| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 그리디
- springdatajpa
- 알고리즘
- Thymeleaf
- spring
- 백준
- java
- jpa
- AOP
- Greedy
- http
- Proxy
- 인프런
- Spring Boot
- Android
- 자바
- Servlet
- 김영한
- db
- 스프링
- pointcut
- QueryDSL
- Exception
- JDBC
- kotlin
- 스프링 핵심 기능
- SpringBoot
- transaction
- JPQL
- 스프링 핵심 원리
- Today
- Total
개발자되기 프로젝트
평균 수행시간이 O(logN)인 알고리즘 : Heap 정렬 & element 추가 본문
평균 수행시간이 O(logN)인 경우 : 한 번 수행할 때 마다 정렬해야 하는 수가 1/2개로 줄어드는 경우
- Quick 정렬(퀵 정렬) : worst인 경우 O(n^2) 까지 가능..
- Merge 정렬(병합 정렬) : 메모리를 가지고 있다. element를 분배한다. 얘네를 다시 병합하면서 sorting
- Heap 정렬(힙 정렬) : Heap 이라는 tree구조. 실제 구현은 배열로 만듦.
단, Merge 정렬과 Heap 정렬은 추가적인 메모리가 필요하다.
0. Heap 정렬
Heap 이란? complite binary tree(BT)를 의미한다.
Complite Binary Tree란? 이진 트리로,
1) 무조건 element가 왼쪽부터 채워져야 하고
2) height가 h라 할 때, h-1까지 fully binary tree이고
3) h부터는 왼쪽부터 채워져야 한다.

element가 빠지거나 들어오며 재정리가 될 때 트리의 특징이 바뀌면 안됨.
즉 기존 Heap이 Min heap 인 경우, parent는 child보다 무조건 작아야 하는 특징이 바뀌면 안된다.
반대로 Max heap은 parent가 자신의 child보다 무조건 커야한다.
sorting은 어떻게? element를 하나 씩 꺼내면 된다.
민힙 상태에서 어센딩 소팅을 하겠다. root element를 하나씩 꺼내는데, 꺼내고 나면 리오더링 해야함.
리오더링에 걸리는 시간이 time complexity. binary tree이기 때문에 O(logN)
1. 배열로 Heap 구현하기
먼저 아래와 같은 Heap이 있다고 가정하자.(10 : min Heap --> parent가 자신의 child보다 커야 작아야 함)

Heap은 배열로 구현할 수 있는데, 아래와 같이 구현이 가능한다.
index 0 은 추후 나누기 2 때문에 사용 안한다.

각 요소의 parent를 찾는 방법은 간단하다! 해당 index를 2로 나눈 몫에 해당하는 index를 찾아가면 된다.
왜냐! 왼쪽 부터 차례대로 들어가고, 다음 줄로 넘어갈 때마다 개수가 2배로 증가하기 때문!
예를들어, 70의 parent를 찾아보자 70의 index는 7이고 2로 나눈 몫은 3이다.
index 3을 찾아가면 20이고 이는 7의 paraent이다.
2. 새로운 element 추가하기.
7을 새로 추가하는 상황을 가정하자.
- 먼저 7은 가장 마지막 자리에 들어간다고 가정하자.
tree로 나타내면 아래와 같다.

배열로 나타내면 다음과 같다. index 9자리에 들어간다.

- parent와 비교하기
그 다음에, parent와 비교를 하자. parent가 child보다 큰 경우 해당 child와 위치를 바꾼다.
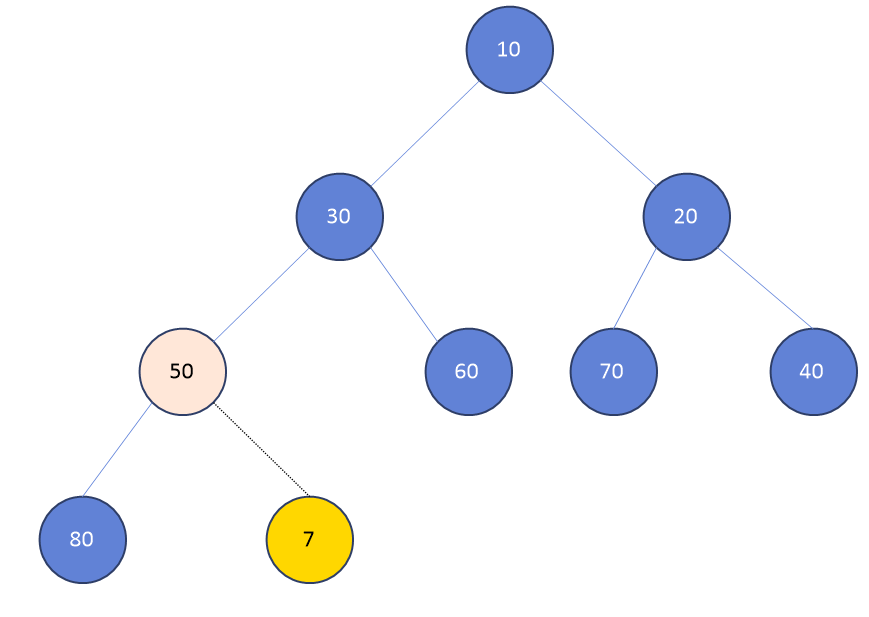
50은 7보다 크다! 위를 바꾸자


다음 parent인 30과 비교하자!

30은 7보다 크다! 바꾸자!


그다음 parent인 10과 비교하자!

10이 더 크다! 바꾸자!


3. 코드로 구현하자
기본적으로 Min Heap인 경우와, Max Heap인 경우는 조건만 달라지면 된다.
parent와 child 비교 시 뭐가 더 클때! 만 정해주면 된다.
public class HeapSort {
private int[] heapArry;
int i = 1; //처음 들어가는 위치 지정을 위해
public HeapSort(){
heapArry = new int [50];
}
public void insertHeap(int input){
heapArry[i] = input;
int index =i; //parent와 반복하여 비교하기 위한 index관리
i++; //다음 element 들어올 때, 맨 뒤에 들어갈 수 있도록.
int temp = 0;
//parent랑 비교해야함.
while(heapArry[(index/2)] > heapArry[index] && index > 1){ // Min Heap
//while(heapArry[(index/2)] < heapArry[index] && index > 1){ //Max Heap
temp = heapArry[index];
heapArry[index] = heapArry[(index/2)];
heapArry[(index/2)] = temp;
index = index/2;
}
}
public static void main(String[] args) {
HeapSort heapSort = new HeapSort();
heapSort.insertHeap(10);
heapSort.insertHeap(30);
heapSort.insertHeap(20);
heapSort.insertHeap(50);
heapSort.insertHeap(60);
heapSort.insertHeap(70);
heapSort.insertHeap(40);
heapSort.insertHeap(80);
System.out.println("Heap : " + Arrays.toString(heapSort.heapArry));
heapSort.insertHeap(7);
System.out.println("7 추가!");
System.out.println("Heap : " + Arrays.toString(heapSort.heapArry));
}
}Min Heap으로 잘 결과가 나온 것을 확인할 수 있다.
Heap : [0, 10, 30, 20, 50, 60, 70, 40, 80, 0, 0, 0, 0, ....., 0, 0, 0, 0, 0, 0, 0, 0, 0]
7 추가!
Heap : [0, 7, 10, 20, 30, 60, 70, 40, 80, 50, 0, 0, 0, ....., 0, 0, 0, 0, 0, 00, 0, 0]
'Java > 알고리즘' 카테고리의 다른 글
| DFS(Depth - Fist Search) : 개념, 예시 (0) | 2021.06.04 |
|---|---|
| 평균 수행시간이 O(logN)인 알고리즘 : Heap 정렬 & element 삭제 (0) | 2021.06.01 |
| 평균 수행시간이 O(n^2)인 알고리즘 (0) | 2021.05.31 |
| 정렬된 수 에서 특정 수의 위치 찾기 : binary search (0) | 2021.05.31 |
| 알고리즘 문제 풀이: min, max 값 찾기 (0) | 2021.05.30 |