| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Exception
- 인프런
- 스프링
- 알고리즘
- Servlet
- 김영한
- JPQL
- Spring Boot
- Greedy
- 그리디
- http
- springdatajpa
- kotlin
- jpa
- SpringBoot
- Proxy
- db
- Thymeleaf
- AOP
- pointcut
- JDBC
- Android
- spring
- 스프링 핵심 원리
- java
- QueryDSL
- 스프링 핵심 기능
- transaction
- 백준
- 자바
- Today
- Total
개발자되기 프로젝트
평균 수행시간이 O(n^2)인 알고리즘 본문
일반적으로 정렬 알고리즘은 O(n^2)의 수행시간을 가짐.
1. Selection Sort
| 50 | 10 | 60 | 80 | 90 | 100 | 20 |
위와같이 숫자 배열이 있을 때, 오름차순으로 정렬해보자
앞에서부터 쭉 스캔해서 제일 작은 값 찾고, 가장 앞에 위치시킴.
다름 위치에는 누굴 데려올까, 쭉 스캔하다가 가장 작은 값 선택(selection)
즉, n개의 값을 n번 씩 봐야 하기 때문에 O(n^2)이다.
2. Bubble Sort
아래와 같이 숫자 배열이 있다고 하자.
| 50 | 10 | 60 | 90 | 80 | 20 | 100 |
1) 50 & 10 비교한다. 10이 더 작다. -->50 ↔ 10 위치 바꾼다.
| 10 | 50 | 60 | 90 | 80 | 20 | 100 |
3) 50 & 60 비교 --> 그대로
| 10 | 50 | 60 | 90 | 80 | 20 | 100 |
5) 60 & 90 --> 순서 바꾸기
| 10 | 50 | 90 | 60 | 80 | 20 | 100 |
6) 60 & 80 --> 그대로
| 10 | 50 | 90 | 60 | 80 | 20 | 100 |
7) 80 & 20 --> 순서 바꾸기
| 10 | 50 | 90 | 60 | 20 | 80 | 100 |
8) 80 & 100 --> 그대로
| 10 | 50 | 90 | 60 | 20 | 80 | 100 |
9) 한 번 진행하면 가장 큰 수가 맨 끝으로 이동됨.
10) 모든 수가 정렬될 때 까지 반복.
11) 즉 한 개의 element가 자리를 잡기 위해 n번 시행하고, element가 n개 이므로 O(n^2)이다.
3. Insertion Sort
손안의 카드! 즉 이미 정렬된 상태에서 새로운 요소를 추가할 때 정렬하는 개념
쉽게 말해 앞에 정렬된 요소들과 비교하여 자기 자리 찾는 방법
아래와 같이 배열이 있다고 하자.

1) 50부터 시작하자. 50은 본인 자리를 그대로 유지
2) 10을 앞에 정렬된 50과 비교하자. 10은 50보다 작다.

3) 50을 옆에 빈칸으로 옮기고 10을 첫 번째 자리에 놓자.

4) 3번째 수인 60을 가지고 시작하자. 바로 앞의 수인 50보다 크다. 60을 50오른쪽에 빈칸에 놓자.
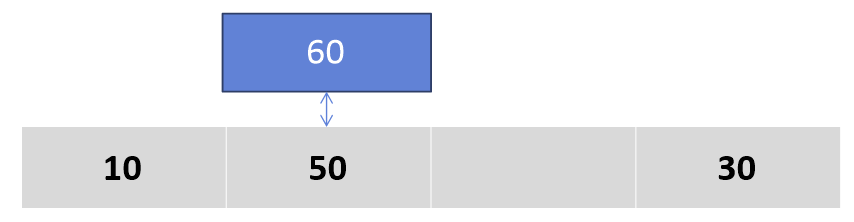

5) 4번 째 수인 30의 위치를 정하자. 바로 앞에 있는 60과 비교하자. 60이 더 크다.

6) 60을 오른쪽으로 옮기고, 30은 50과 비교하자. 30이 더 작다.
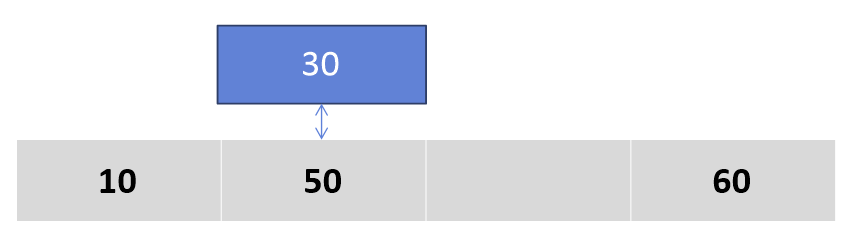
7) 50을 오른쪽으로 옮기고, 30은 10과 비교하자.

8) 30은 10보다 크다. 30을 10 오른쪽에 놓자.

9) 정렬이 끝났다.

즉, 하나의 element가 자리를 잡기 위해 비교하는 횟수가 n에 dependent하고.
n개의 element가 있기 때문에 O(n^2) 이다.
<예시>
public class InsertionSort {
public static void main(String[] args) {
int[] arr = {84,32,81,50,62,48,92,21};
System.out.println("원래 배열 : " + Arrays.toString(arr));
insertionSort(arr);
}
public static void insertionSort(int[] arr){
int temp = 0;
for(int i = 1; i < arr.length; i++){
temp = arr[i];
//arr[i] = 0;
for(int j = i-1; j >=0; j--){
if(arr[j] > temp){
arr[j+1]= arr[j];
arr[j] = temp;
}
}
}
System.out.println("정렬된 배열 : " + Arrays.toString(arr));
}
}
코드 실행 결과
원래 배열 : [84, 32, 81, 50, 62, 48, 92, 21]
정렬된 배열 : [21, 32, 48, 50, 62, 81, 84, 92]흠.. 값은 잘 나왔지만 엄격히 말하면 Insertion Sort와는 다르다.
내가 짠 코드는 앞의 요소와 계속 비교하며 자리를 바꿔나가지만..
Insertion Sort는 정확한 위치를 찾은 뒤 자리를 변경한다.
즉, temp의 위치를 결정하는 코드가 temp보다 작은 값을 찾은뒤에 나와야 한다.
그렇게 하기 위해서는 for문보다는 while문을 써서 arr[j-1] > temp인 경우에 계속 돌게 만들면 될 듯 하다.
public class InsertionSort {
public static void main(String[] args) {
int[] arr = {84,32,81,50,62,48,92,21};
System.out.println("원래 배열 : " + Arrays.toString(arr));
insertionSort(arr);
}
public static void insertionSort(int[] arr){
int temp = 0;
for(int i = 1; i < arr.length; i++){
temp = arr[i];
int j = i;
while((j >=1) && arr[j-1] > temp){
arr[j] = arr[j-1];
j=j-1;
}
arr[j] = temp;
}
System.out.println("정렬된 배열 : " + Arrays.toString(arr));
}
}위와 같은 결과가 나왔다.
원래 배열 : [84, 32, 81, 50, 62, 48, 92, 21]
정렬된 배열 : [21, 32, 48, 50, 62, 81, 84, 92]'Java > 알고리즘' 카테고리의 다른 글
| DFS(Depth - Fist Search) : 개념, 예시 (0) | 2021.06.04 |
|---|---|
| 평균 수행시간이 O(logN)인 알고리즘 : Heap 정렬 & element 삭제 (0) | 2021.06.01 |
| 평균 수행시간이 O(logN)인 알고리즘 : Heap 정렬 & element 추가 (0) | 2021.06.01 |
| 정렬된 수 에서 특정 수의 위치 찾기 : binary search (0) | 2021.05.31 |
| 알고리즘 문제 풀이: min, max 값 찾기 (0) | 2021.05.30 |