Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- Thymeleaf
- JDBC
- Exception
- http
- pointcut
- 알고리즘
- spring
- Android
- 인프런
- 백준
- Proxy
- 스프링
- JPQL
- springdatajpa
- Spring Boot
- SpringBoot
- 자바
- QueryDSL
- 스프링 핵심 기능
- AOP
- 그리디
- kotlin
- db
- 스프링 핵심 원리
- Greedy
- 김영한
- Servlet
- jpa
- transaction
- java
Archives
- Today
- Total
개발자되기 프로젝트
[프로그래머스] 피보나치 수 본문
1. 문제
피보나치 수는 F(0) = 0, F(1) = 1일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 적용되는 수 입니다.
예를들어
- F(2) = F(0) + F(1) = 0 + 1 = 1
- F(3) = F(1) + F(2) = 1 + 1 = 2
- F(4) = F(2) + F(3) = 1 + 2 = 3
- F(5) = F(3) + F(4) = 2 + 3 = 5
와 같이 이어집니다.
2 이상의 n이 입력되었을 때, n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴하는 함수,
solution을 완성해 주세요.
제한 사항
- n은 2 이상 100,000 이하인 자연수입니다.
입출력 예
| n | return |
| 3 | 2 |
| 5 | 5 |
입출력 예 설명
피보나치수는 0번째부터 0, 1, 1, 2, 3, 5, ... 와 같이 이어집니다.
2. 문제 정리, 초기 접근
- n번째 피보나치수를 1234567로 나눈 "나머지"를 확인하는 문제.
- 피보나치 수는 급격하게 증가한다.
- 따라서 int에는 값을 담지 못할 것으로 예상한다.
- 따라서 피보나치수는 long으로 담아두자.
3..코드 : 초기접근
class Solution {
public long solution(int n) {
int number = 1234567;
long f1 = 0;
long f2 = 1;
int cnt = 1;
long answer=0;
if(n<2){
return 1;
}
while(cnt<=n){
cnt++;
long f = f1 + f2;
f1 = f2;
f2 = f;
//System.out.println(f);
if(cnt == n) {
answer = f%1234567;
break;
}
}
return answer;
}
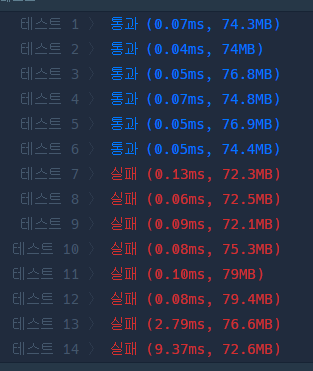
}하지만 절반은 실패한다. 로직은 맞는 것 같은데 형식에 문제가 있는 것 같다.
피보나치 수는 그 값이 급격하게 증가하기 때문에 long에도 담지 못하나??
4. 코드 변경
- 그렇다면 메모리를 차지하는 양을 줄여보자.
- 결국 얻어야 하는 값은 피보나치 수를 1234567로 나눈 나머지이다.
- 즉 이 말은 피보나치수를 모두 1234567로 나눈 나머지로 컨트롤하면 된다는 뜻.
class Solution {
public long solution(int n) {
int number = 1234567;
long f1 = 0 % number;
long f2 = 1 % number;
int cnt = 1;
long answer=0;
if(n<2){
return 1;
}
while(cnt<=n){
cnt++;
long f = (f1 + f2)%number;
f1 = f2;
f2 = f;
//System.out.println(f);
if(cnt == n) {
answer = f;
break;
}
}
return answer;
}
}

5. GitHub : 211220 Fibonacci
GitHub - bsh6463/coding_test
Contribute to bsh6463/coding_test development by creating an account on GitHub.
github.com
'코테준비' 카테고리의 다른 글
| [백준] Greedy : 설탕배달 (0) | 2022.05.15 |
|---|---|
| 코테준비 (0) | 2022.05.11 |
| [프로그래머스] JadenCase 문자열 만들기 (0) | 2021.12.20 |
| [프로그래머스] 카카오프레즈 컬러링북 (0) | 2021.12.19 |
| [프로그래머스] 문자열 압축 (0) | 2021.12.17 |
Comments

