
유선청소기 요즘 대세는 바로 이것
👉유선청소기 1등 제품👈
목차
유선청소기 추천 순위
안녕하세요.
오늘은 유선청소기 최고로 인기 있는 제품들을 소개드리려고 합니다.
올해 기준 판매량이 가장 많고 긍정적인 후기가 많은 상품들로 엄선해 보았습니다.
유선청소기 추천 상품들을 확인해보세요!
유선청소기 추천 TOP10
품절 또는 제품 없음 시 아래 최신 상품 보러가기를 클릭해주세요
 일렉트로룩스 얼티밋 홈 700 싸이클론 진공청소기, EFC71511DB, 데님블루★★★★★ 최저가 219,000원  |
 대웅모닝컴 싸이클론 유선 진공청소기, DWM-4733C, 혼합색상★★★★★ 최저가 52,300원  |
 마이뉴 유선 진공청소기 MVC-600WT, 화이트★★★★★ 최저가 31,800원  |
 홈플래닛 2 IN 1 유선 청소기, 화이트, MC607B★★★★★ 최저가 20,490원  |
 일렉트로룩스 얼티밋 홈 700 싸이클론 진공청소기, EFC71511BP, 블러쉬 핑크★★★★★ 최저가 239,000원  |
 [최신형] 신일 업소용 청소기 흡입력 좋은 건습식 진공청소기 20L 30L, SVC-DK20L, 혼합 색상★★★★★ 최저가 129,000원  |
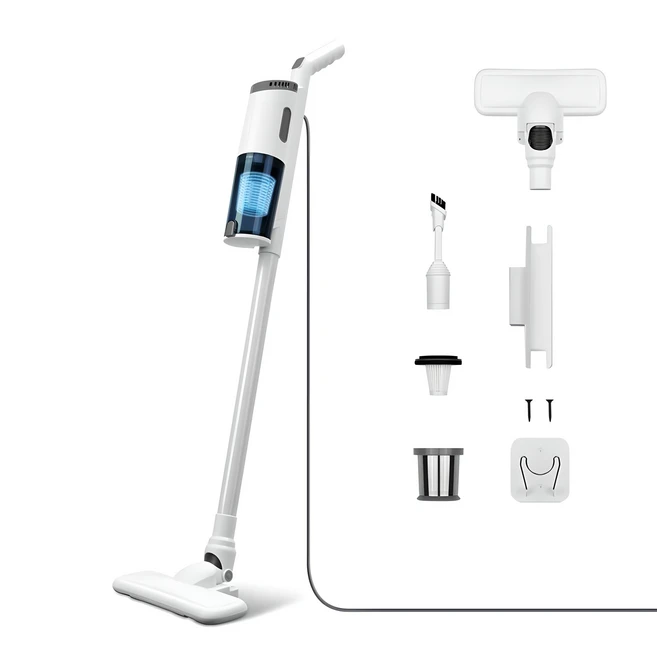 홈리아 룸가드 유선 진공청소기, HA-13KW, 화이트★★★★★ 최저가 39,900원  |
 2025년형 유선 청소기 600W 길이조절 연장봉 초강력 경량 다용도 화이트, 혼합, 색상:혼합★★★★★ 최저가 48,900원  |
 넥소버 2in1 핸디+스틱 유선 진공청소기 가정용 사무실 원룸 청소기 미니 소형 청소기, NXV-501A★★★★★ 최저가 39,900원  |
 미디어 2in1 스틱 앤 핸디형 유선 진공 청소기, SC861B, 블랙★★★★★ 최저가 22,900원  |
유선청소기 BEST 제품 포스팅을 끝까지
읽어주셔서 진심으로 감사드립니다.
오늘도 즐겁고 행복한 하루되셨으면 좋겠습니다!
유선청소기 추천 연관 키워드
상표권 게시물 삭제는 댓글 또는 구글폼을 이용하시면 됩니다.
⭐게시물 삭제 요청⭐
맺음말
1위 추천 제품은 일렉트로룩스 얼티밋 홈 700 싸이클론 진공청소기, EFC71511DB, 데님블루 입니다.
2위 추천 제품은 대웅모닝컴 싸이클론 유선 진공청소기, DWM-4733C, 혼합색상 입니다.
3위 추천 제품은 마이뉴 유선 진공청소기 MVC-600WT, 화이트 입니다.
4위 추천 제품은 홈플래닛 2 IN 1 유선 청소기, 화이트, MC607B 입니다.
5위 추천 제품은 일렉트로룩스 얼티밋 홈 700 싸이클론 진공청소기, EFC71511BP, 블러쉬 핑크 입니다.
좋은 상품 선택하셔서 즐거운 쇼핑 되시길 바랍니다.

