| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 자바
- 알고리즘
- pointcut
- http
- 인프런
- jpa
- JDBC
- QueryDSL
- Android
- Proxy
- Exception
- Greedy
- Servlet
- db
- JPQL
- spring
- 스프링 핵심 기능
- transaction
- kotlin
- Thymeleaf
- 스프링 핵심 원리
- 백준
- 스프링
- SpringBoot
- Spring Boot
- AOP
- java
- springdatajpa
- 김영한
- 그리디
- Today
- Total
개발자되기 프로젝트
최단거리 구하기 : Dijkstra algorithm 본문
시작 노드에서 전체 노드로 가는 최단 거리를 구하는 알고리즘.
이 알고리즘을 시행하면 시작노드부터 각 노드까지 최단 거리를 알 수 있다.
특징으로는 각 단계를 반복하면서 시작노드부터의 각 노드까지 최단 거리를 계속 업데이트 한다.
현재 노드를 기준으로,
기존에 입력된 weight(현재 노드를 거치지 않음)가 더 작은지
현재 노드를 거치는게 weight가 작은지 비교해야한다.
즉 노드 v에 인접한 노드 w에 대하여 아래 조건이 성립하면 w에 대한 최단거리를 업데이트 한다.
(원래 w로 가는 거리보다 v를 거쳐서 가는 거리가 가까우면 w가는 거리를 v거쳐서 가는 거리로 수정.)
Yv + Cvw < Yw --> Yw = Yv + Cvw
ex) Y1 + C1,2 < Y2
그 결과로 알고리즘이 종료되었을 때, 시작노드를 기준으로 각 노드 까지의 최단거리를 구할 수 있는 것이다.

1. 예시
1) 시작노드는 0이고 0과 인접한 node까지의 weight를 입력한다.

2) 두 인접 노드 중 weight가 적은 곳을 선택한다. 0은 이미 방문했으니 제외하면 가장 작은 weight는 1이다.
즉, 다음 노드는 1이다.
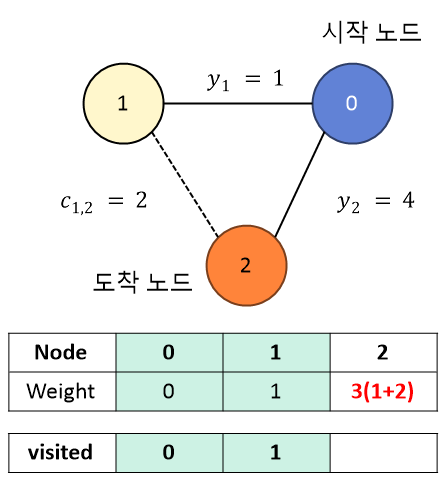
여기가 중요! 기존에 바로 2로 가는 거리(weight)와 "1"을 거쳐서 갈 경우의 거리(weight)를 비교한다.
1을 거쳐갈 경우가 작으면 weight 업데이트가 필요하다.
이 경우에는,0 -> 1- > 2의 weight가 3으로 , 0 --> 2의 weight 4보다 작다. 따라서 2의 weight를 업데이트 한다.
3) 이제 가장 작은 weight는 3으로 다음 node는 2이다. 0을 기준으로 모든 노드에 대한 최단거리를 알았다.

4) 알고리즘을 시행 후 노드2에 대한 최단거리가 변경되었다.
0에서 바로 가는 것 보다 1을 거쳐 가는 방법이 거리(weight)가 작다.
2. 좀더 구체적인 사례로 보자.
1) 0부터 시작하고, 0노드 기준으로 거리를 입력한다. 연결이 안된 노드는 ∞로 입력.


2) 0을 제외하고 가장 weight가 낮은 노드는 1이다.
위의 노드2에 해당하는 weight는 0에서 바로 2로 갈 경우의 weight이다.
하지만 1을 거쳐서 노드2로 갈때 거리(weight)가 바로 2로 가는 경우보다 낮다. 업데이트 해주자.


3) 다음으로 가장 작은 노드는 2이다.
이미 방문한 0과 1을 제외한 인접 노드(바로 갈수있는 노드) 까지 거리를 업데이트한다.
이 경우엔 노드3이 유일하고. 3까지 가는 최단 거리는 2를 거쳐서 가는 방법 말고는 없다.

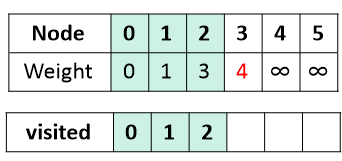
4) 3을 기준으로 같은 행위를 반복
3과 바로 연결된 노드는 노드 4, 5이다. 해당 노드를 가기 위해서는 3을 거쳐가야한다.


5) 그다음 가장 작은 weight인 5를 기준으로.
3에서 4로 바로 가는 것 보다. 5를 거져갈 때 weight가 줄어든다.


6) 마지막 남은 노드 4를 기준으로.
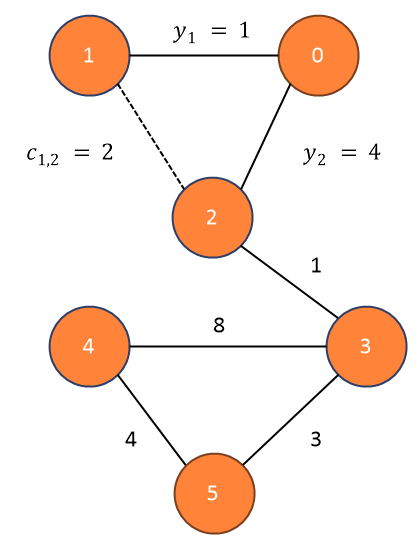

7) 알고리즘이 모두 종료되었고, 각 노드까지의 최단거리를 알 수 있다.
'Java > 알고리즘' 카테고리의 다른 글
| 미로 찾기! (0) | 2021.06.10 |
|---|---|
| 최단거리 구하기 : Dijkstra algorithm 코드로 구현 (0) | 2021.06.08 |
| BFS(Breadth-First Search) 너비 우선 탐색 개념 (0) | 2021.06.06 |
| DFS(Depth - Fist Search) : 코드로 구현 (0) | 2021.06.04 |
| DFS(Depth - Fist Search) : 개념, 예시 (0) | 2021.06.04 |



